Algorithms
What are Algorithms?
An algorithm is a well-defined sequence of steps or instructions designed to perform a specific task or solve a particular problem. Algorithms are fundamental to computer science and programming and can be used in a wide variety of applications, from simple calculations to complex data processing tasks.
Bubble Sort
Bubble Sort is the easiest sorting algorithm, where it compares to adjacent elements to see which one is bigger then swaps them. And repeats the process.
Time Complexity: O(n^2) , Space Complexity: O(1)
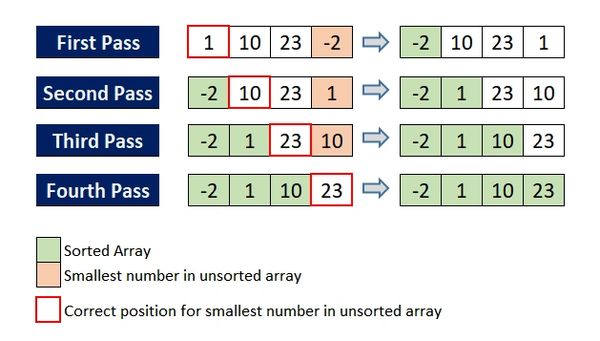
Selection Sort
Selection Sort is also another easy sorting algorithm to use, but similar to bubble sort it is also not that efficient with larger test cases. Selection sort finds the smallest or largest element and swaps it with the first unsorted element and it repeats.
Time Complexity: O(n^2) , Space Complexity: O(n^2)
Insertion Sort
Insertion Sort is another easy algorithm that is suitable for small test case but becomes inefficient when the case is larger. It Builds the sorted list one element at a time by repeatedly taking the next element and inserting it into the correct position.
Time Complexity: O(n^2) , Space Complexity: O(n)
Quick Sort
Quick Sort is one of the most popular sorting algorithm from its efficient use case. It Picks a pivot element, partitions the list into elements less than and greater than the pivot, and recursively sorts the partitions. It is build using 2 functions the main quickSort function, the recursive part, and the partition where the calculation occurs.
O(n log n) on average, but O(n²) in the worst case.
Heap Sort
Heap Sort is a comparison-based sorting algorithm that uses a binary heap data structure to sort elements. it is really efficient and doesn't require extra memory so using this in C/C++, where memory management is important, is really beneficial. But this sorting algorithm isn't that stable.
Time Complexity: O(n log n), Space Complexity: O(1)
Linear Search
Linear Search is the simplest searching algorithm to learn. What it does is it iterates through each element in the collection sequentially until the target element is found.
Complexity: O(n), where n is the number of elements in the array.
Binary Search
The Binary Search is another really straight forward search algorithm. It finds the middle element of the array and checks if the target element is smaller or larger then the middle element and splits the array in half until it finds the target.
Complexity: O(log n) in the worst case, where n is the number of elements in the collection.
Depth-First Search (DFS):
Depth-First Search is another searching algorithm but is used in primarily in trees or graphs. It Explores as far as possible along each branch of the search tree before backtracking.
Complexity: O(V + E), where V is the number of vertices and E is the number of edges in the graph.
Breadth-First Search (BFS):
Breadth-First Search (BFS) is similar to the Depth-First Search whereas it explores all the neighbor nodes at the present depth before moving to the next level instead of the farthest possible branch. Used primarily for tree or graph data structures.
Complexity: O(V + E), where V is the number of vertices and E is the number of edges in the graph.